SULLE CONDIZIONI DI EQUILIBRIO DINAMICO
DI UN SISTEMA DI MASSE ROTANTI

 

   Siano M ed MI   le masse non uguali di due corpi tra loro solidalmente collegati e liberi di ruotare attorno all'asse o, e siano l ed lI   le rispettive distanze dei loro baricentri dall'asse di rotazione. Per semplicità si trascura la massa propria del vincolo di collegamento e si suppone che i due corpi siano puntiformi e quindi le loro masse siano concentrate nei rispettivi baricentri.

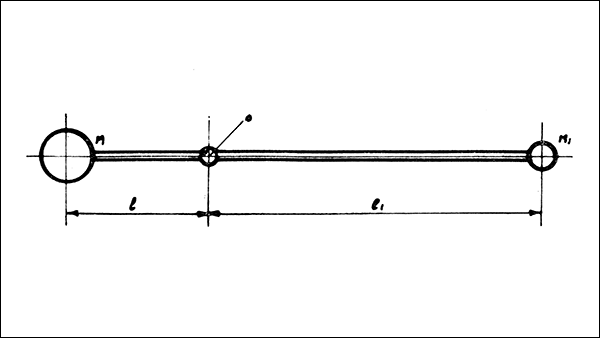
   Nelle trattazioni di meccanica applicata, un sistema di questo tipo viene generalmente considerato dinamicamente equilibrato quando, oltre alla condizione di equilibrio statico data da

sia verificata anche la condizione che la retta passante per i baricentri delle due masse sia normale all'asse di rotazione.
   In tali condizioni, effettivamente, le forze centrifughe generate dalla rotazione delle masse e rappresentate da

 e 

sono evidentemente uguali di intensità, coincidenti nella direzione e opposte nel verso e quindi si elidono reciprocamente senza dar luogo, durante il moto rotatorio uniforme, ad altre reazioni sul perno (col quale si potrebbe materializzare l'asse) che non siano quelle dovute al peso, ove questo esista, proprio delle medesime masse rotanti.
   Ma la considerazione è inficiata dalla limitazione dell'esame delle forze centrifughe, o inerziali, nella sola ipotesi del moto uniforme, giacché estendendo l'esame a un moto vario, comunque accelerato, risulterebbe che il momento della forza inerziale opponentesi alla coppia accelerante non è uguale per le due masse M ed MI .
   Infatti tale momento, resistente o motore a seconda del segno dell'accelerazione, è dato per la massa M da

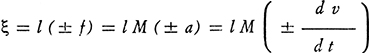
ove f è la forza inerziale resistente o motrice, t il tempo in cui avviene la variazione di moto e v la velocità lineare del baricentro della massa M.
   Analogamente, il momento della forza inerziale della massa MI  è dato da

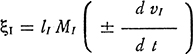
   Ora, essendo per ipotesi l ≠ lI, e quindi v ≠ vI, nonché l M = lI MI, sarà conseguentemente ξ ≠ ξI.
   Se poi si preferisse partire da una rappresentazione schematica più concreta di quanto non sia il precedente modello, si potrebbe considerare la rotazione di un solido prismatico ed eterogeneo attorno a un asse normale all'asse del prisma e passante per il baricentro del prisma stesso. Si considerino allora le due bande del prisma, di massa M e MI, idealmente separate da un piano normale all'asse del prisma e comprendente l'asse di rotazione, e si ammetta che le distanze l e lI dei baricentri propri di ogni banda dal baricentro del prisma siano disuguali. In tal caso, essendo l'asse di rotazione baricentrico, è verificata la condizione iniziale Ml = MIlI, e risulta intuitivamente l'uguaglianza, rispetto alle due bande, dei momenti statici di l'ordine e per ciò stesso, la disuguaglianza dei momenti inerziali di 2° ordine.
   Ne consegue che all'azione di una indeterminata coppia acceleratrice o deceleratrice reagirebbe non soltanto una coppia inerziale resistente o, rispettivamente, motrice, ma anche una ulteriore forza la quale determinerebbe il mancato equilibrio dinamico del sistema nel perdurare del moto vario. Il vettore di tale forza perturbatrice sarebbe infatti rotante con le masse e quindi atto a determinare praticamente quei moti vibratori che sono peculiari di tale sistema, il quale è dinamicamente equilibrato solo in relazione al moto uniforme e pertanto può essere più propriamente definito dinamicamente pseudoequilibrato.
Le condizioni di equilibrio dinamico assoluto di un sistema di masse rotanti sono dunque:
   1. che l'asse di rotazione sia baricentrico;
   2. che la risultante delle forze centrifughe elementari sia nulla;
   3. che siano uguali i momenti d'inerzia, rispetto all'asse di rotazione, delle due bande assiali del sistema, comunque orientate.

 

   Dattiloscritto senza indicazione della data, attribuibile all'ottobre 1958. Non risulta se sia stato oggetto di pubblicazione.