PARALOGISMI DELLA TEORIA DELLA RELATIVITÀ

 

Da Trieste, il 24 aprile del 1970

   Illustrissimo professor Cester,
   Ricordo che, l'ultima volta che ebbi il piacere d'incontrarla, Ella ebbe la bontà di intrattenermi esponendomi, per quanto succintamente, alcune conseguenze che si sarebbero dovute trarre dalla teoria della relatività di Einstein, e ricordo pure che, in quell'occasione, io osai dirle che tali conseguenze, e quindi, presumibilmente, la teoria medesima, mi sembravano inficiate da contraddizioni.
   Queste contraddizioni, in verità, a me sembrano numerose e non del tutto inconsistenti, sicché sarei ora tentato di parlargliene, ma, per non abusare della Sua cortesia e per non esorbitare dai limiti epistolari, mi sforzerò di accennare soltanto, e con la maggior concisione possibile, ad alcune di esse attinenti alla contrazione del tempo in funzione della velocità.
   Si dice che, secondo la teoria relativistica, se fosse possibile attuare l'esperimento dei «fratelli gemelli», e cioè lasciare uno dei due fratelli sulla Terra e far partire l'altro su una nave spaziale orbitante attorno alla Terra a grandissima velocità per un tempo sufficientemente lungo, si dovrebbe constatare, al rientro sulla Terra della nave stessa, che i due fratelli non sarebbero più coevi e precisamente che il navigatore, per effetto della contrazione del tempo subita durante la navigazione, sarebbe più giovane dell'altro. In altri termini, se i due fratelli possedessero orologi assolutamente precisi, e inizialmente regolati sulla stessa ora, alla fine dell'esperimento i due orologi non segnerebbero più la stessa ora perché per l'uno il tempo è trascorso più lentamente che per l'altro.
   A questo proposito io vorrei chiedere cosa succederebbe se il fratello sulla Terra e quello sulla nave potessero, anziché usare due distinti orologi, servirsi entrambi, e in qualsiasi momento, del medesimo orologio. Questa interrogazione non è, in effetti, riferita a una condizione irrealizzabile come potrebbe sembrare perché un tale ipotizzato orologio comune realmente esiste. Il suo quadrante, infatti, è costituito dall'eclittica terrestre che, al pari degli orologi usuali, si può immaginare porti la numerazione dall'I al 12 (il 3 e il 9 agli equinozi, il 6 e il 12 ai solstizi), con la sola differenza che questi numeri, invece delle ore, segnerebbero i mesi dell'anno. E vi è pure la lancetta indicatrice il cui perno è materializzato dal Sole e la cui estremità è materializzata dalla Terra che compie esattamente un giro di quadrante all'anno (tropico).
   Orbene, la velocità tangenziale del moto orbitale della Terra essendo mediamente , se ne dovrebbe dedurre che il periodo di un orologio terrestre è più lungo di quello di un orologio gemello collocato (per ipotesi!) sul Sole, tanto da assumere, rispetto a questo ultimo, il valore

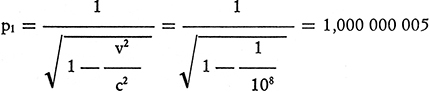
   Se dunque, per la Terra orbitante, il periodo si allungasse (e quindi il tempo si contraesse) di 5/109 = 1/2 . 108  rispetto al periodo solare, bisognerebbe ammettere che la Terra (che si calcola giri attorno al Sole da circa 5 miliardi di anni) abbia compiuto, dal tempo della creazione,

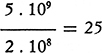
giri in più attorno al Sole di quanti non ne abbia visti il Sole compiere dalla Terra attorno a sé.
   Una tale ammissione sembra poco accettabile e ancor meno lo sembrerà quando si consideri che, durante i 5 miliardi di anni di esistenza del sistema solare, per ben 25 volte dovrebbe essersi verificato lo strano fenomeno per cui un ipotetico abitante della Terra avrebbe potuto vedere il Sole in congiunzione col Capricorno proprio nel momento in cui un ipotetico abitante del Sole avrebbe potuto vedere la Terra sfasata di mezzo giro orbitale e cioè essa stessa in congiunzione col Capricorno anziché in congiunzione col Cancro.
   Un'eventuale obiezione contro questa mia argomentazione immagino possa essere la seguente: che la sopra menzionata equazione einsteiniana non è applicabile al caso considerato della nave spaziale (e quindi nemmeno della Terra orbitante) perché tale caso contempla moti circolari o quasi circolari (cioè moti relativi in cui la distanza dei due laboratori di controllo resta pressoché invariata per tutta la durata dell'esperimento) e che l'esempio dei fratelli gemelli viene sì talvolta prospettato, ma al solo scopo di fornire un'immagine delle conseguenze del fenomeno e non già del fenomeno stesso.
   Se tale fosse l'obiezione, non avrei alcuna difficoltà ad accettarla, ma allora vorrei mi fosse acconsentito di prendere in esame anche il caso di moti relativi rettilinei e uniformi.
   Si supponga dunque che in una stazione spaziale A, non rotante, si abbiano tre orologi (I, II, III) assolutamente identici, precisi, sincroni e regolati sulla stessa ora. Si supponga inoltre che l'orologio I permanga alla stazione A, mentre gli altri due orologi, il II e il III, siano, a un certo momento, fatti partire con un missile B diretto lungo una traiettoria rettilinea con velocità (rispetto alla stazione A) costante v. Orbene, durante la corsa del missile B, gli orologi II e III, a esso solidali, non potranno più, secondo la teoria relativistica, mantenere il sincronismo con l'orologio I, cosicché, se il periodo di questo ultimo fosse N, il periodo degli orologi II e III (che restano tra loro sincroni) diverrebbe

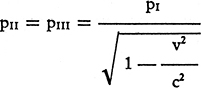
E se poniamo

si avrebbe

   A questo punto mi sembra opportuno soffermare l'attenzione su questo piccolo mondo del missile B con i suoi due orologi. Qui il tempo dovrebbe scorrere meno velocemente che nella stazione A di partenza, ma, finché non interverranno cause perturbatrici del suo moto traslatorio rettilineo e uniforme, esso costituirà, al pari della stazione A, un mondo a sé e il suo sistema inerziale resterà invariato. Per questo mondo non possono quindi esserci, come non ce ne sono per la stazione A, direzioni preferenziali, cosicché se da esso, a un certo momento, facessimo partire un piccolo missile C (che praticamente potremmo considerare come il secondo stadio del missile B), la successiva contrazione del tempo che in questo missile C dovrebbe verificarsi rispetto al tempo misurato sul missile B, a causa della sua velocità a quest'ultimo relativa, dovrebbe essere determinata esclusivamente dal valore numerico di tale velocità e quindi essere del tutto indipendente dalla direzione e senso della velocità stessa.
   Se dunque, assieme al missile C e con velocità costante vI  = v facciamo partire lungo una traiettoria rettilinea l'orologio III, lasciando l'orologio II sul missile B, dovrebbe accadere che l'aumento del periodo dell'orologio III, rispetto a quello dell'orologio II, sia identico all'aumento di periodo subito dall'orologio II rispetto all'orologio I, ovvero si avrebbe

e ciò qualsiasi sia la direzione e il senso della velocità vI.
   Senonché, se lanciassimo questo missile C nella stessa direzione ma senso contrario al lancio del missile B, accadrebbe che il valore vettoriale della velocità dell'orologio III rispetto a quello dell'orologio I diverrebbe

e ne conseguirebbe che l'orologio III resterebbe immobile rispetto
all'orologio I, cosicché, in questa nuova condizione, questi due orologi
devono necessariamente esser tra loro sincroni e cioè deve essere

il che è in patente contraddizione col sopra indicato risultato derivante
dall'applicazione della teoria relativistica.
   Vorrei ancora osservare che non mi sembra possibile eludere la suddetta contraddizione introducendo il paralogismo secondo cui, pur essendo vI = v, può non essere vI  — v = 0, e dico ciò perché, in tal caso, per eludere una contraddizione se ne pone una nuova. Infatti la suddetta eguaglianza esprime una verità non deduttiva ma tautologica, e quindi avulsa dall'ambito dell'opinabile, perché la sua negazione altro non sarebbe che mera contraddizione in termini.
   Illustrissimo Professore, suppongo che in tutto quello che ho detto non vi sia probabilmente alcunché di originale, e di ciò mi scuso assicurandola che l'unico motivo che mi ha spinto a scrivere queste righe è quello di compiere il tentativo di chiarire a me stesso alcuni problemi appassionanti. Naturalmente non mi aspetto da Lei, occupato in ben più gravi e importanti impegni, una risposta scritta, ma Le sarei veramente molto grato se, con tutto comodo, volesse, un giorno o l'altro, esser tanto cortese da telefonarmi indicandomi, per sommi capi, gli errori che avrà rilevato nella mia breve esposizione.
   Voglia intanto gradire le mie più cordiali espressioni e credermi

Il Suo devotissimo
Oliviero Mogno

 

 

Da Trieste, il 18 aprile del 1979

Ai Servizi Speciali del TG1 Via Teulada, 66 - Roma

Oggetto: Quesito sulla teoria della relatività

   Ho seguito col più vivo interesse la Vostra trasmissione di qualche tempo fa concernente la teoria einsteiniana della relatività e ora, se ancora in tempo, vorrei accogliere il cortese invito, rivolto agli ascoltatori, di scrivervi esprimendo liberamente le loro osservazioni in proposito.
   Io vorrei soffermarmi sul concetto della relatività del tempo, da Voi esemplificato in modo tanto suggestivo con la parabola dei due fratelli gemelli e, a tal proposito, vorrei raccomandare alla benevola attenzione del chiarissimo professor Zichichi la considerazione del seguente caso ipotetico.
   Mettiamo che i gemelli siano tre: Elio, Deuterio e Trizio. Elio rimane sulla Terra mentre Deuterio e Trizio partono con una astronave, che ha una velocità di crociera di 125.000 km/sec, puntando sulla stella Canopus. Il conto alla rovescia avviene il 1° gennaio dell'anno 2500, nel giorno stesso in cui i tre fratelli compiono il loro trentesimo anno d'età.
   Non appena raggiunta la velocità di crociera (il che, mediante dispositivi ai nostri tempi ancora ignoti, si suppone che avvenga in brevissimo tempo), Deuterio dice a Trizio:
   «Il nostro viaggio, secondo i cronometri che si trovano sulla Terra, dovrà avere esattamente la durata di dieci anni, cosicché saremo di ritorno il giorno del quarantesimo compleanno di nostro fratello Elio. Ma quel giorno noi due non potremo festeggiare assieme a lui il nostro quarantesimo compleanno perché, viaggiando alla velocità costante di 125.000 km/sec, per noi il tempo trascorre più lentamente. Secondo quanto disse sei secoli or sono il famoso Albert Einstein, l'allungamento del tempo è per noi del 10% sicché, nel giorno di rientro, noi ci troveremo ad essere di circa un anno più giovani di Elio».
   «Quello che mi dici, risponde Trizio, mi fa molto piacere perché io ho sempre avuto gran timore della vecchiaia».
   «Ma se questa è la tua preoccupazione, soggiunge Deuterio, tu potresti invecchiare ancor più lentamente di me. Basterà che tu parta da questa astronave servendoti della navetta di salvataggio la quale, come questa astronave, ha una propria velocità di crociera di 125.000 km/sec. In tal modo tu invecchierai tanto più lentamente di me quanto io invecchierò più lentamente di nostro fratello Elio».
   «Bene, conclude Trizio, accetto con entusiasmo di fare l'esperimento. Ma resta ancora un punto da stabilire e cioè: quale direzione dovrò prendere?».
   «Agli effetti del nostro esperimento, lo rassicura Deuterio, ciò non può avere alcuna importanza, così come non poteva avere alcuna importanza la direzione che abbiamo preso partendo dalla Terra. Perché tu non devi dimenticare che noi due su questa astronave, ci troviamo in un nostro esclusivo sistema inerziale e quindi, come in ogni altro sistema inerziale, non può esservi alcuna direzione preferenziale».
   Addunque, dopo un ulteriore conto alla rovescia, Trizio parte con la sua navetta e memore, se pur non del tutto convinto dei ragguagli fraterni, decide di viaggiare in senso opposto a quello dell'astronave ovvero di puntare verso la Terra cosicché, terminata la breve fase di accelerazione, egli si trova a viaggiare alla velocità costante di circa 125.000 km/sec rispetto alla primitiva astronave, ma in senso contrario a essa e quindi a permanere, per tutto il decennio dell'esperimento, a una distanza pressoché costante dalla Terra.
   Come prestabilito, il 1° gennaio del 2.510 i nostri navigatori dello spazio arrivano simultaneamente alla stazione terrestre ove Elio li accoglie festosamente. Deuterio e Trizio brindano, oltreché al successo dell'impresa, al quarantesimo compleanno di Elio. Ed Elio, ancora ignaro dell'avventurosa sortita di Trizio, brinda ai 39 anni dei suoi fratelli.
   Ma, in tale festoso evento, quanti anni ha veramente Trizio? Forse 39, come crede Elio; oppure 38, come suppone Deuterio; oppure 40, come egli stesso sospetta?
   Ben grato se vorrete essere tanto cortesi da illuminarmi su questo interrogativo, Vi prego di gradire le più cordiali espressioni di saluto del Vostro obbligatissimo

Oliviero Mogno